In the rapidly evolving field of quantum computing, researchers are continuously seeking methods that push the boundaries of what classical computers can achieve. A recent collaboration between experts from Freie Universität Berlin, University of Maryland, Google AI, and others has sought to address one of the most perplexing challenges in quantum simulation: the accurate estimation of Hamiltonian parameters associated with bosonic excitations in superconducting quantum simulators. This pursuit may lead to profound implications for both theoretical understanding and practical applications in quantum technologies.
The genesis of this research can be traced back to a phone call Jens Eisert, the lead author of the foundational paper, received during a conference in Brazil. Friends from the Google AI team were encountering significant hurdles while trying to calibrate their advanced superconducting quantum chip, Sycamore. Initially, Eisert believed the solutions would be straightforward—however, the complexity of the problem soon became apparent. The team faced difficulties in obtaining accurate frequency estimations of the Hamiltonian, which impeded their ability to identify essential parameters from the available data.
Realizing the depth of the challenge, Eisert enlisted the expertise of several brilliant Ph.D. students, forming a collaborative team dedicated to unraveling the complexities of Hamiltonian learning. The initial optimism quickly transformed into a multi-year project filled with rigorous experimentation and theoretical exploration as they sought to establish a reliable methodology.
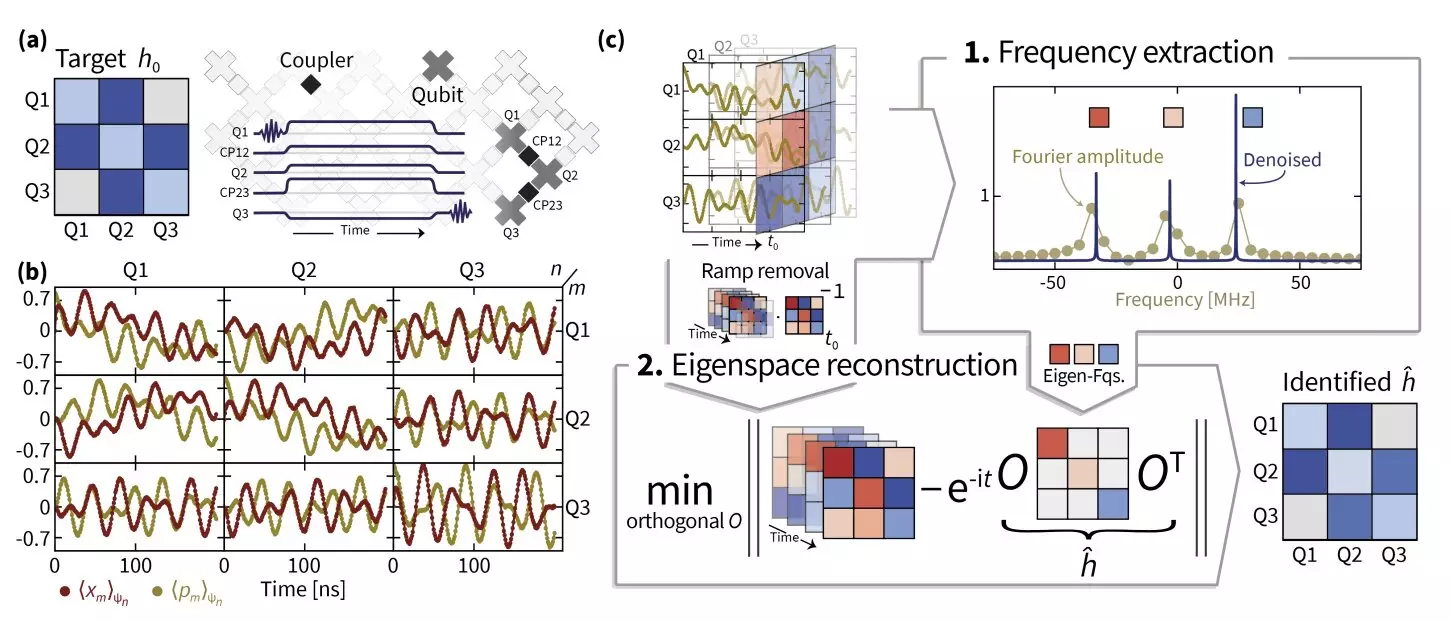
At the crux of their breakthrough were techniques that enhanced the resolution of Hamiltonian dynamics estimation. The researchers employed superresolution—a method typically used in imaging—to fine-tune eigenvalue estimation. This allowed them to achieve clarity in the Hamiltonian parameters that were previously obscured by noise and inaccuracies in experimental data.
Further, they implemented manifold optimization, a sophisticated technique designed to work with data in curved spaces rather than the standard Euclidean framework. This nuanced approach was pivotal in accurately retrieving the eigenspaces of the Hamiltonian operator, enabling the team to put forward an effective recovery of the Hamiltonian itself.
Eisert emphasized the importance of understanding the dynamics involved in manipulating quantum systems, highlighting that the transition processes in quantum operations are inherently imperfect. Acknowledging these imperfections, the team developed “TensorEsprit,” a new signal processing method. This technique proved incredibly effective even with larger systems, marking a significant advance in the field of Hamiltonian learning.
The findings presented in their research indicate promising scalability of the proposed methodologies. The ability to robustly identify Hamiltonian parameters for up to 14 superconducting qubits across two processors paves the way for its application in larger quantum systems. As researchers advance into the next phases of their work, they aim to apply these techniques to complex interacting quantum systems and extend their research to encompass cold atom experiments, building upon foundational work pioneered by physicist Immanuel Bloch.
Eisert notes that while many researchers have traditionally assumed the Hamiltonian of a system is known, this assumption often does not hold in practice. The importance of accurately characterizing a Hamiltonian cannot be overstated; it is crucial for predictive capability in quantum mechanics, lending urgency to the quest for reliable methods to learn Hamiltonians directly from experimental data.
The implications of this research extend far beyond theoretical frameworks. By refining the techniques used to characterize analog quantum simulators, the researchers could catalyze the development of high-precision quantum simulations, ultimately enhancing our understanding of complex quantum systems and materials. Analog quantum simulations allow researchers to study intricate phenomena under controlled laboratory conditions, presenting an exciting avenue for new discoveries in science.
As Eisert aptly puts it, the questions surrounding the nature of Hamiltonians and their identification play a critical role in the broader discourse of quantum mechanics. The coming years are likely to witness a shift in focus toward more practical applications arising from these investigations. Innovations like TensorEsprit are not mere academic exercises; they hold the potential to inform the design and functionality of next-generation quantum devices.
The collaborative efforts of this research team illuminate the intricate dance of Hamiltonian learning within superconducting quantum systems. By achieving a robust method for estimating Hamiltonian parameters, they contribute not just to fundamental science but also to the burgeoning field of quantum technologies. Future endeavors promise to lead to a deeper understanding of analog quantum simulators and offer the potential for high-precision simulations that could transform research across various scientific domains. As the field continues to grow, the importance of accurately characterizing Hamiltonians will only increase, making this a pivotal area of study for years to come.